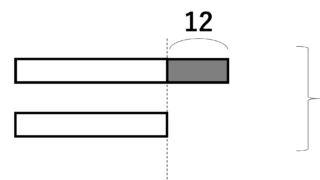こんにちは！スマホパパ(@plus30blog)です。
現在、中学受験生の子どもと日々奮闘中！
私&妻の中学受験の経験を活かしつつ、令和の中学受験に対応するため、積極的に情報収集をし、また経験してわかったことを書いています。
そのおかげか、子どもは『勉強嫌い』から『勉強好き』に変わりました！うちの子に必要だったもの合わなかったもの、とにかく調べたことはつらつらと書いていきます。
中学受験の算数では、特殊算と呼ばれる独特な問題が多く出題されます。特殊算をしっかり攻略することで、算数の成績をぐんと伸ばすことができます。今回は、特殊算の種類とその攻略方法について、わかりやすくお話しします。
本題の前に…
子どもが本を読まない、時事ネタを子どもに解説するのが大変。我が家はそんな悩みがありましたが、読売KODOMO新聞を購読してみたところと一発解決！時事ネタを中心にした内容でフルカラー、四谷大塚・ねこねこ日本史・名探偵コナン・ポケモンが協力したページで読みやすい！しかも週１回発行で月額550円(税込）とコスパもGood。親もこっそり勉強できて(笑)、まさか子どもと時事ネタで会話することもでてきました！
2冊プレゼント！11/29まで
はじめに
中学受験算数の特殊算をマスターするには、各種類の問題の特徴と解き方をしっかり理解することが大事です。これにより、試験での得点力をグッと上げることができます。
特殊算は、中学受験の算数でよく出る重要な問題です。それぞれの問題には独自の解き方があり、これを理解することで、試験本番でも自信を持って取り組むことができます。
特殊算の基本的な解き方はここで紹介しますが、解き方を忘れてしまった時や、このページでの解き方で対応できなかった時は、我が家で実践している万能な別の解き方があります。
特殊算の種類とその攻略方法
以下に、中学受験算数の特殊算の代表的な種類と、その攻略方法を紹介します。
旅人算
旅人算は、2人以上が違う速さで移動する問題です。例えば、「AさんとBさんがそれぞれ反対方向に歩き始めると何時間後に出会うか」などです。
攻略方法:
速さ、時間、距離の関係（速さ＝距離÷時間）をしっかり理解する。
2人の距離の合計が一定になることを使って解く。
例えば、AさんとBさんが30km離れた地点から出発し、それぞれ時速5kmと時速3kmで向かい合って歩く場合、二人が出会うまでの時間は、二人の速さを足して8km/hになります。この速度で30kmを進むので、30km÷8km/h＝3.75時間、つまり3時間45分で出会うことがわかります。
通過算
通過算は、電車や列車がトンネルや橋を通過する問題です。例えば、「長さ100mの電車が長さ200mのトンネルを通過するのにかかる時間を求めよ」などです。
攻略方法:
電車や列車の全長とトンネルや橋の長さを合計して考える。
通過にかかる時間を求めるために、速さを活用する。
例えば、時速60kmの電車が100mのトンネルを通過する場合、電車の長さが200mだとすると、電車がトンネルを完全に通過するまでの距離は200m＋100m＝300mです。時速60kmは秒速に直すと60km×1000m÷3600秒＝16.67m/sです。よって、300mを通過するのにかかる時間は300m÷16.67m/s＝18秒となります。
植木算
植木算は、一定間隔で植えられた木や立てられた柱の数を数える問題です。「直線上に10mおきに木を植えると、50mの距離には何本の木が必要か」などです。
攻略方法:
端の木の本数や柱の数に注意する。
両端に木がある場合とない場合で数え方が異なることを理解する。
例えば、50mの距離に10mおきに木を植える場合、50÷10＝5ではなく、6本の木が必要です。これは両端に木がある場合の数え方で、最初の木を1本目として、10mごとに次の木を植えていくためです。
濃度算
濃度算は、濃度や割合の計算に関する問題です。「100mlの食塩水に塩を加えて濃度を何％にするか」などが出題されます。
攻略方法:
基本的な濃度の公式（濃度＝溶質の量÷全体の量×100）を使いこなす。
濃度の変化を追って計算する。
例えば、100mlの10％の食塩水にさらに20gの塩を加えると、全体の量は100ml＋20g＝120mlになります。このときの濃度は（10g＋20g）÷120ml×100＝25％になります。
ニュートン算
ニュートン算は、仕事や作業の問題で、一定時間でどれだけの仕事ができるかを求めます。「A機械が1時間で30個の製品を作り、B機械が1時間で20個の製品を作る場合、2台の機械で何時間かかるか」などです。
攻略方法:
仕事量の合計とそれぞれの作業速度を基に、全体の仕事量を割り出す。
同時に作業する場合の合計速度を利用して解く。
例えば、A機械が1時間で30個、B機械が1時間で20個の製品を作るとします。両方の機械を同時に動かすと、1時間で30個＋20個＝50個の製品が作れます。もし100個の製品を作るのにかかる時間は、100個÷50個/時＝2時間となります。
倍数算
倍数算は、ある数量が他の数量の何倍かを問う問題です。例えば、「Aさんの年齢はBさんの年齢の3倍です。Aさんが36歳のとき、Bさんは何歳か」などです。
攻略方法:
基本的な倍数の概念を理解する。
比の計算を活用して解く。
例えば、Aさんの年齢がBさんの3倍で36歳なら、Bさんの年齢は36歳÷3＝12歳です。
割合算
割合算は、ある数量の中に含まれる割合を求める問題です。例えば、「全体の40％が男性で、男性の人数が120人の場合、全体の人数を求めよ」などです。
攻略方法:
割合の基本的な計算（全体の量×割合＝部分の量）を活用する。
パーセントを小数に直して計算する。
例えば、全体の40％が男性で120人なら、全体の人数は120人÷0.40＝300人です。
消去算
消去算は、2つ以上の式を使って一つの変数を消去して解く問題です。例えば、「x＋y＝10、2x＋3y＝20を解く」などです。
攻略方法:
2つの式を使って一つの変数を消去する。
残った変数を解いて答えを求める。
例えば、x＋y＝10、2x＋3y＝20の式から、まずxを消去するために、1つ目の式を2倍して2x＋2y＝20を作り、2x＋3y＝20から引くと、yが消えてy＝0になります。このyの値を使ってxを求めるとx＝10になります。
比算
比算は、2つ以上の数量の比率を使って計算する問題です。例えば、「3：2の比率で分けた金額が1500円の場合、それぞれの金額を求めよ」などです。
攻略方法:
基本的な比率の概念を理解する。
合計を使って各部分の値を計算する。
例えば、3：2の比率で分けた金額が1500円なら、全体を5（3＋2）と考えて、3部分は1500円×3/5＝900円、2部分は1500円×2/5＝600円になります。
場合の数
場合の数は、物事が起こる可能な組み合わせを数える問題です。例えば、「3つの色を使って塗る場合の組み合わせは何通りあるか」などです。
攻略方法:
基本的な組み合わせや順列の計算を理解する。
必要に応じて公式を使う。
例えば、3つの色を使って2つの物を塗る場合、組み合わせは3×2＝6通りです。ただし、色の順番が重要でない場合は、同じ組み合わせが繰り返されるので、組み合わせを計算する必要があります。
数列算
数列算は、数列の規則性を見つけて、次の数字や合計を求める問題です。「1, 3, 6, 10, …の数列の次の数を求めよ」などです。
攻略方法:
数列の規則を見つける。規則に基づいて計算を進める。
例えば、1, 3, 6, 10,…の数列は、n番目の数が1＋2＋…＋nで表されることがわかります。次の数は15（10＋5）になります。
立体図形の表面積と体積
立体図形の表面積と体積は、立体図形の表面積や体積を求める問題です。「高さ3cm、底面の半径2cmの円柱の体積を求めよ」などです。
攻略方法:
基本的な立体図形の公式（例えば、円柱の体積＝底面積×高さ）を覚える。
各辺や面の長さを正確に計算する。
各図形の基本的な公式をおさらいしたい方はこちら
速さの変化算
速さの変化算は、速さが変わる場面の計算です。例えば、「ある区間を速さ5km/hで歩き、残りを10km/hで走るときの平均速度を求めよ」などです。
各区間の時間を求め、全体の時間で平均速度を計算する。
時間の和と距離の和を使って平均速度を求める。
攻略方法:
例えば、10kmの道のりを5km/hで2時間歩き、残りを10km/hで1時間走る場合、平均速度は全体の距離（10km）÷全体の時間（3時間）＝3.33km/hになります。
Point（再提示）
特殊算を攻略するためには、各種類の問題の特徴を理解し、それぞれの解法を身につけることが大切です。これにより、試験での得点力が格段に向上します。
例えば、高さ3cm、底面の半径2cmの円柱の体積は、底面積（2×2×3.14=12.56cm2）に高さをかけて、答えは12.56×3=37.68cm2になります。
連立方程式
連立方程式は、2つ以上の方程式を同時に解く問題です。「x＋y＝10、2x－y＝4を解く」などです。
攻略方法:
2つの式を使って一方の変数を消去する。
残った変数を解いて答えを求める。
例えば、x＋y＝10、2x－y＝4の式から、まずyを消去するために、2つの式を足して、3x＝14となり、x＝14/3＝4.67。次に、xの値を使ってyを求めると、y＝10－4.67＝5.33になります。
確率算
確率算は、ある出来事が起こる確率を求める問題です。「サイコロを振って3が出る確率を求めよ」などです。
攻略方法:
確率の基本的な公式（起こる可能性のある事象の数÷全ての事象の数）を理解する。
各可能性を正確に数える。
例えば、サイコロを振って3が出る確率は、1/6（6つの面のうち1つが3）になります。
まとめ
中学受験の算数で特殊算をマスターすることは、成績アップに直結します。今回ご紹介した各特殊算の特徴と攻略方法を参考に、しっかりと準備を進めましょう。親子で協力して取り組むことで、受験の成功に一歩近づくことができます。
今回の記事が、少しでも皆さんのお役に立てれば幸いです。特殊算の攻略方法をマスターし、中学受験を成功させるために、今からしっかりと準備を進めていきましょう。成功を祈っています！
お読みいただきありがとうございました！
最後に、
テレビ東京が、中学受験の塾や私立中学の紹介を動画配信しているのを知っていましたか？｢円卓のコンフィデンシャル｣という番組は中学受験の特集を何度もしています。いつもテーマが秀逸で、大·小の塾代表や過去問作成会社、ママライターなど最新情報を持っている方々に「先取り学習の是非」「本番にピークに持っていくには」「第一志望のみ徹底対策はアリ？ナシ？」「保護者の心得」などをテーマに直球対談。この動画を配信しているテレ東Bizでは、他にもTHE名門校･ガイアの夜明け･カンブリア宮殿･WBS･モーサテも！
＼7日間無料で見放題！／